Ministerul Educatiei, Cercetarii, Tineretului si Sportului
Centrul National de Evaluare si Examinare
Examenul de bacalaureat 2011
Proba E. c)
Proba scrisa la Matematica
Filiera vocationala, profilul militar, specializarea matematica - informatica.
Toate subiectele sunt obligatorii. Se acorda 10 puncte din oficiu.
Timpul efectiv de lucru este de 3 ore.
La toate subiectele se cer rezolvari complete.


Din inegalitatile de mai sus rezulta ca 2 este singurul numar intreg din intervalul dat.
2.Axa de simetrie a unei parabole este dreapta de ecuatie
Stiind din ipoteza ca axa de simetrie a parabolei este x=2 obtinem ca:

3.Deoarece 1/2 este in intervalul inchis [-1,1] rezulta ca ecuatia trigonometrica data are solutii.


Dam apoi valori lui k (numere intregi)si retinem doar acele valori ale lui x in intervalul [0,2 pi).
Pentru k=0 obtinem:

Pentru k=1 obtinem:

Pentru alte valori intregi ale lui k(pozitive si negative) se obtin valori ale lui x in afara intervalului [0,2 pi).
In concluzie singurele solutii ale ecuatiei date din intervalul [0,2 pi) sunt:
 4.
4.
!}=\frac{1\cdot2\cdot3\cdot...\cdot\left ( n-2 \right )\left ( n-1 \right )n}{1\cdot2\cdot1\cdot2\cdot3\cdot...\cdot\left ( n-2 \right )}=\frac{\left ( n-1 \right )\cdot n}{2})
!}=\frac{1\cdot2\cdot3\cdot...\cdot\left ( n-2 \right )\left ( n-1 \right )n}{1\cdot2\cdot3\cdot...\cdot\left ( n-2 \right )}=\left ( n-1 \right )\cdot n)
Ecuatia data in exercitiu devine:
\cdot n}{2}+\left ( n-1 \right )\cdot n=18\Leftrightarrow n^2-n+2n^2-2n=36 \Leftrightarrow 3n^2-3n-36=0 \\ \Leftrightarrow n^2-n-12=0)
Se rezolva aceasta ecuatie de gradul doi si se obtin solutiile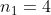 si
si 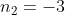 dintre care singura solutie acceptabila este
dintre care singura solutie acceptabila este 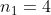 tinand cont de ipoteza.
tinand cont de ipoteza.
5.Dreptele date in exercitiu sunt paralele daca si numai daca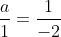 de unde se obtine
de unde se obtine 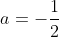 .
.
6.Egalitatea data in exercitiu se transforma echivalent astfel:
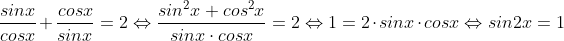 ceea ce trebuia demonstrat.Am folosit mai sus formula fundamentala a trigonometriei(vezi formule trigonometrice)
ceea ce trebuia demonstrat.Am folosit mai sus formula fundamentala a trigonometriei(vezi formule trigonometrice)

\cdot A\left ( y \right )=\begin{pmatrix} 1 & x & x^2\\ 0 & 1 & 2x\\ 0& 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & y & y^2\\ 0& 1 &2y \\ 0& 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & x+y & x^2+2xy+y^2\\ 0& 1 & 2x+2y\\ 0&0 & 1 \end{pmatrix}=\\= \begin{pmatrix} 1 & x+y & \left ( x+y \right )^2\\ 0& 1 & 2\left ( x+y \right )\\ 0&0 & 1 \end{pmatrix}=A\left ( x+y \right ))
b)Facem scaderea din paranteza:
-A\left ( y \right )= \begin{pmatrix} 1 & x &x^2 \\ 0& 1& 2x\\ 0& 0 & 1 \end{pmatrix}- \begin{pmatrix} 1 & y &y^2 \\ 0& 1& 2y\\ 0& 0 & 1 \end{pmatrix}= \begin{pmatrix} 0& x-y &x^2-y^2 \\ 0& 0 &2\left ( x-y\right ) \\ 0& 0 & 0 \end{pmatrix})
Ridicam matricea obtinuta la puterea a doua apoi la puterea a treia:
-A\left ( y \right ) \right )^2= \begin{pmatrix} 0& x-y &x^2-y^2 \\ 0& 0 &2\left ( x-y\right ) \\ 0& 0 & 0 \end{pmatrix}\cdot \begin{pmatrix} 0& x-y &x^2-y^2 \\ 0& 0 &2\left ( x-y\right ) \\ 0& 0 & 0 \end{pmatrix}= \begin{pmatrix} 0 &0 &2\left ( x-y \right )^2 \\ 0&0 &0 \\ 0& 0 &0 \end{pmatrix})
-A\left ( y \right ) \right )^3= \left (A\left ( x \right )-A\left ( y \right ) \right )^2\cdot \left (A\left ( x \right )-A\left ( y \right ) \right )=O_3) .
.
In concluzie-A\left ( y \right ) \right )^k=O_3,\forall k\geq 3\Rightarrow \left ( A\left ( x \right )-A\left ( y \right ) \right )^ \left{ 2011 \right}=O_3) c.c.t.d.
c.c.t.d.
c)Matricea A(x) este inversabila deoarece determinantul ei este egal cu 1 si deci este diferit de 0.
Din egalitatea demonstrata la punctul a) deducem ca:
\cdot A\left ( -x \right )= A\left (-x \right )\cdot A\left ( x \right )=A\left ( 0 \right )=I_3) Aceasta arata ca:
Aceasta arata ca:
 \right )^{-1}=A\left ( -x \right )=\begin{pmatrix} 1 &-x &x^2 \\ 0& 1 &-2x \\ 0&0 & 1 \end{pmatrix})
2.a)Calculam f(-1):
=\left ( -1 \right )^3+\left ( 1-\alpha \right )\left ( -1 \right )^2+\left ( \alpha -2 \right )i \left ( -1 \right )+\alpha +\left ( \alpha -2 \right )i=\\ =-1+1-\alpha -\alpha i +2i +\alpha +\alpha i-2i=0)
de unde rezulta ca polinomul f are radacina x=-1.
b)Daca radacinile lui g sunt numere complexe conjugate atunci ele au forma:
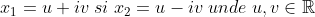
Din relatiile lui Viete obtinem:
\left ( u-iv \right )=u^2+v^2=q \end{matrix}\right}.)
Mai departe avem:

Ecuatia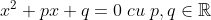 are radacini distincte complexe conjugate daca si numai daca
are radacini distincte complexe conjugate daca si numai daca 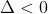 .
.
Rezulta ca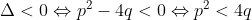 c.c.t.d.
c.c.t.d.
c)Deoarece polinomul f are radacina x=-1(conform puuncului a) rezulta din teorema lui Bezout ca f este divizibil cu x+1 si deci se poate descompune in factori astfel:
\left ( X^2-\alpha X +\alpha +\left ( \alpha -2 \right )i \right ))
Polinomul f are doua radacini complexe conjugate daca paranteza are doua radacini complexe conjugate.
Conform punctului b) rezulta cai\in \mathbb{R}) de unde obtinem ca
de unde obtinem ca 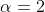 valoare pentru care paranteza are
valoare pentru care paranteza are 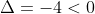 si deci f are doua radacini complexe conjugate.
si deci f are doua radacini complexe conjugate.
In concluzie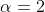 .
.

Calculam deci derivata functiei f.
=\left [ ln\left ( x+1 \right ) \right -ln\left ( x-1 \right ) ]'=\frac{1}{x+1}-\frac{1}{x-1}=\\=\frac{x-1-x-1}{x^2-1}=-\frac{2}{x^2-1})
Observam ca daca x>1 atunci f '(x)<0 de unde rezulta ca functia data este strict descrescatoare pe intervalul)
b)Cautam asimptota orizontala la graficul functiei f spre + infinit.
= \lim_{x\rightarrow +\infty}\left ( ln\left ( x+1 \right ) -ln\left ( x-1 \right )\right )=\lim_{x\rightarrow +\infty}\left ( ln\frac{x+1}{x-1} \right )=\\ =ln\left ( \lim_{x\rightarrow +\infty}\frac{x+1}{x-1} \right )=ln1=0)
Rezulta ca graficul functiei date are asimptota orizontala catre + infinit dreapta de ecuatie y=0(adica axa Ox).
Daca graficul are asimptota orizontala spre + infinit atunci nu are asimptota oblica spre + infinit.
Mai departe cautam asimptota verticala in punctul de abscisa x=1.
= \lim_{x\rightarrow 1;x>1}ln\frac{x+1}{x-1}=ln\frac{2}{0+}=ln\left ( +\infty\right )=+\infty)
deci graficul are asimptota verticala dreapta de ecuatie x=1.
Functia f este continua pe intervalul) deci nu are alte asimptote verticale.
deci nu are alte asimptote verticale.
c)Limita data devine:
= \lim_{x\rightarrow +\infty}x\left [ ln\left ( x+1 \right ) -ln\left ( x-1 \right )\right ]\overset{ \left (+\infty \cdot 0 \right ) }{=}\\ =\lim_{x\rightarrow +\infty}\frac{ln\left ( x+1 \right ) -ln\left ( x-1 \right )}{\frac{1}{x}}\overset{ \left (\frac{0}{0} \right ) }{=}) Pentru calculul acestei limite aplicam regula lui l'Hospital si obtinem:
Pentru calculul acestei limite aplicam regula lui l'Hospital si obtinem:
 }{=}\\) Se ma aplica o data regula lui l'Hospital si se obtine rezultatul final astfel:
Se ma aplica o data regula lui l'Hospital si se obtine rezultatul final astfel:
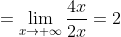 2.a)Pentru calculul integralei definite date procedam in felul urmator:
2.a)Pentru calculul integralei definite date procedam in felul urmator:
 b)Intai sa observam ca functia f este negativa pe intervalul [1;2] si deci si functia g va fi negativa pe intervalul [1;2].
b)Intai sa observam ca functia f este negativa pe intervalul [1;2] si deci si functia g va fi negativa pe intervalul [1;2].
Aria determinata de graficul functiei g cu axa Ox se va calcula astfel:
 c)Rezolvarea acestui exercitiu se poate face cu un artificiu putin diferit de cel dat in baremul de corectare, in felul urmator:
c)Rezolvarea acestui exercitiu se poate face cu un artificiu putin diferit de cel dat in baremul de corectare, in felul urmator:
dx=\int_{1}^{2}\left ( x-\frac{3}{2} \right )'f^n\left ( x \right )dx=)
Se foloseste mai departe metoda integrarii prin parti pentru integrale definite si obtinem:
 Mai departe se trece totul in membrul stang si rezulta:
Mai departe se trece totul in membrul stang si rezulta:
 Prin inmultirea intregii egalitati cu 2 rezulta ceea ce trebuia demonstrat.
Prin inmultirea intregii egalitati cu 2 rezulta ceea ce trebuia demonstrat.
Centrul National de Evaluare si Examinare
Examenul de bacalaureat 2011
Proba E. c)
Proba scrisa la Matematica
Varianta 5
Filiera teoretica, profilul real, specializarea matematica - informatica.Filiera vocationala, profilul militar, specializarea matematica - informatica.
Toate subiectele sunt obligatorii. Se acorda 10 puncte din oficiu.
Timpul efectiv de lucru este de 3 ore.
La toate subiectele se cer rezolvari complete.

Rezolvare subiectul 1:
1.
Din inegalitatile de mai sus rezulta ca 2 este singurul numar intreg din intervalul dat.
2.Axa de simetrie a unei parabole este dreapta de ecuatie

Stiind din ipoteza ca axa de simetrie a parabolei este x=2 obtinem ca:

3.Deoarece 1/2 este in intervalul inchis [-1,1] rezulta ca ecuatia trigonometrica data are solutii.


Dam apoi valori lui k (numere intregi)si retinem doar acele valori ale lui x in intervalul [0,2 pi).
Pentru k=0 obtinem:

Pentru k=1 obtinem:

Pentru alte valori intregi ale lui k(pozitive si negative) se obtin valori ale lui x in afara intervalului [0,2 pi).
In concluzie singurele solutii ale ecuatiei date din intervalul [0,2 pi) sunt:

Ecuatia data in exercitiu devine:
Se rezolva aceasta ecuatie de gradul doi si se obtin solutiile
5.Dreptele date in exercitiu sunt paralele daca si numai daca
6.Egalitatea data in exercitiu se transforma echivalent astfel:

Rezolvare subiectul 2:
1.a)Facem inmultirea celor doua matrice(inmultim linii cu coloane):b)Facem scaderea din paranteza:
Ridicam matricea obtinuta la puterea a doua apoi la puterea a treia:
In concluzie
c)Matricea A(x) este inversabila deoarece determinantul ei este egal cu 1 si deci este diferit de 0.
Din egalitatea demonstrata la punctul a) deducem ca:
2.a)Calculam f(-1):
de unde rezulta ca polinomul f are radacina x=-1.
b)Daca radacinile lui g sunt numere complexe conjugate atunci ele au forma:
Din relatiile lui Viete obtinem:
Mai departe avem:
Ecuatia
Rezulta ca
c)Deoarece polinomul f are radacina x=-1(conform puuncului a) rezulta din teorema lui Bezout ca f este divizibil cu x+1 si deci se poate descompune in factori astfel:
Polinomul f are doua radacini complexe conjugate daca paranteza are doua radacini complexe conjugate.
Conform punctului b) rezulta ca
In concluzie

Rezolvare subiectul 3:
1.a)Pentru a se studia monotonia unei functii se calculeaza derivata acelei functii.Calculam deci derivata functiei f.
Observam ca daca x>1 atunci f '(x)<0 de unde rezulta ca functia data este strict descrescatoare pe intervalul
b)Cautam asimptota orizontala la graficul functiei f spre + infinit.
Rezulta ca graficul functiei date are asimptota orizontala catre + infinit dreapta de ecuatie y=0(adica axa Ox).
Daca graficul are asimptota orizontala spre + infinit atunci nu are asimptota oblica spre + infinit.
Mai departe cautam asimptota verticala in punctul de abscisa x=1.
deci graficul are asimptota verticala dreapta de ecuatie x=1.
Functia f este continua pe intervalul
c)Limita data devine:

Aria determinata de graficul functiei g cu axa Ox se va calcula astfel:

Se foloseste mai departe metoda integrarii prin parti pentru integrale definite si obtinem:

