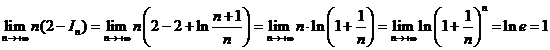Soluţii

Subiectul 1

1..

2.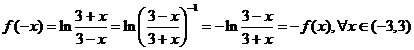 deci funcţia este impară.

3.Ecuaţia ataşată inecuaţiei date este:

care are rădăcinile şi .

Se face tabelul cu semnul funcţiei de gradul doi şi se obţine soluţia .

4.25 de numere sunt divizibile cu 4

20 de numere sunt divizibile cu 5

5 de numere sunt divizibile cu 4 şi 5

Deci 40 numere sunt divizibile cu 4 sau cu 5.

5.Fie .

Avem

şi

MNPQ este paralelogram şi

Punctul căutat este .

6.Semiperimetrul triunghiului ABC este .

Aria triunghiului ABC se calculează cu formula lui Heron:

.

Soluţii

Subiectul 2

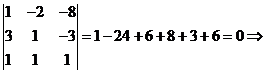1.a) rang

rang.

b) Determinantul caracteristic este:

d_c=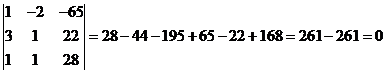, sistemul este compatibil simplu nedeterminat.

Luăm .

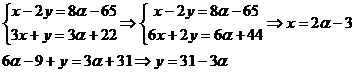
Solutia sistemului este: 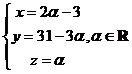.Sistemul este compatibil simplu nedeterminat.

c) 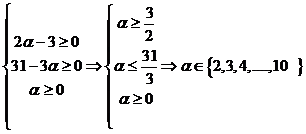, deci sistemul are 9 solutii in multimea

2.a) iar deci .

Rezultă că mulţimea A are 25 de elemente.

b)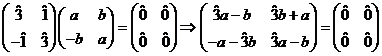

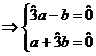care are o soluţie şi deci putem lua de exemplu .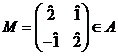

c)Dacă atunci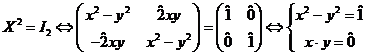

Cazul 1.Dacă atunci deci obţinem matricele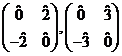

Cazul 2.Dacă atunci şi mai obţinem matricele .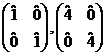

In total ecuaţia are 4 soluţii scrise mai sus.

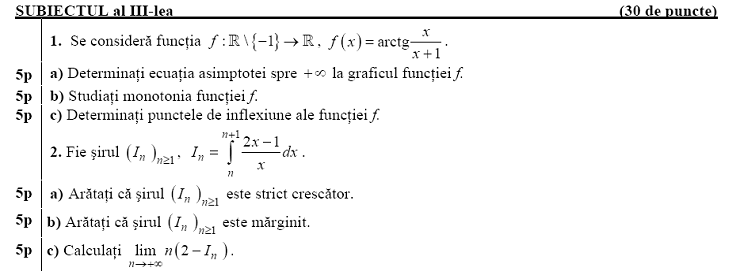
Soluţii

Subiectul 3

1.a)Căutăm asimptotă orizontală:

deci graficul funcţiei are asimpotă orizontală spre de ecuaţie

.

Observaţie:Dacă graficul are asimptotă orizontală spre atunci nu mai are asimptotă oblică spre .

b)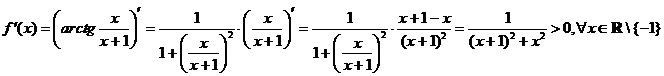

deci funcţia este strict crescătoare pe intervalele şi .

c)

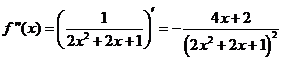
Tabelul cu semnul derivatei a doua este:

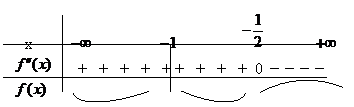
Din tabelul de variaţie rezultă că funcţia f are un singur punct de inflexiune şi anume x= .

2.

.

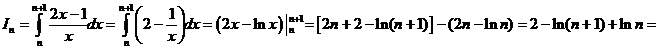
a)

este strict crescător.

b) deoarece şirul este crescător.

, deci sirul este mărginit.

c)