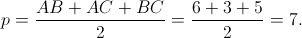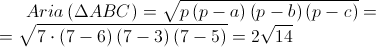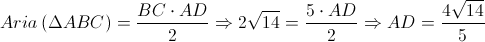Varianta 9 din 30 iunie 2010 comentata (M1)
Sa facem cateva comentarii asupra variantei cu numarul 9 data la examenul de bacalaureat la matematica in data de 30 iunie 2010 la profilul matematica-informatica (M1). Proba scrisa este compusa din trei grupe mari de subiecte,fiecare de cate 30 de puncte,10 puncte fiind date din oficiu. Sa incepem cu Subiectul 1 care este format din 6 exercitii,fiecare de cate 5 puncte.
Primul exercitiu este cu numere complexe:
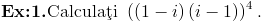
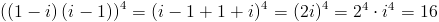
Am folosit aici proprietatile numarului complex i si anume:
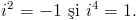
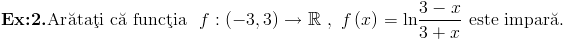
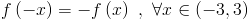
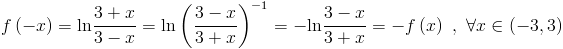
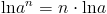
Prin barem se dadeau doua puncte pentru inlocuirea lui x cu -x,alte doua puncte pentru folosirea proprietatii logaritmilor si un punct pentru finalizare. Al treilea exercitiu cerea rezolvarea unei inecuatii de gradul doi in multimea numerelor intregi.
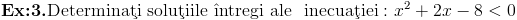
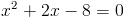
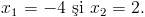
Se face apoi tabelul cu semnul functiei de gradul doi din care rezulta ca solutiile intregi ale inecuatiei date sunt:
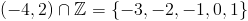
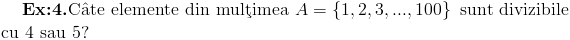
In multimea A sunt 20 de numere divizibile cu 5 si anume 5,10,15,...,100.
Sa observam ca cele doua multimi de mai sus nu sunt disjuncte,ci au elemente comune si anume 20,40,60,80,100.
Elementele din multimea A divizibile cu 4 sau cu 5 sun in numar de 25+20-5=40.
La acest calcul am tinut cont de formula
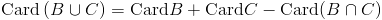
Se mai dadeau doua puncte pentru finalizare. Al cincilea exercitiu este de geometrie de clasa a X-a din lectia "Coordonalete unui vector in plan".
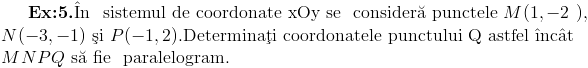
Calculam coordonatele vectorilor
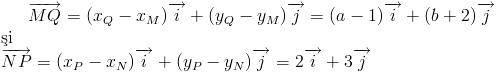
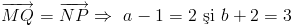 Obtinem ca punctul cautat este Q(3,1).
Obtinem ca punctul cautat este Q(3,1).In barem se dau doua puncte pentru aflarea coordonatelor vectorilor
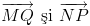
Se mai dau doua puncte pentru conditia de egalitate a celor doi vectori si inca un punct pentru finalizare.
Exercitiul 6 este un exercitiu de geometrie.