Morfisme si izomorfisme de grupuri
Definitie:Fie
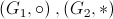 doua grupuri.
doua grupuri.O functie
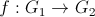 se numeste morfism (monomorfism) de grupuri daca
se numeste morfism (monomorfism) de grupuri daca
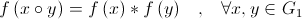
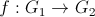 se numeste izomorfism de grupuri daca sunt indeplinite conditiile:
se numeste izomorfism de grupuri daca sunt indeplinite conditiile:- f este morfism de grupuri;
- f este bijectiva;
Doua grupuri
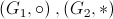 se numesc izomorfe daca intre ele exista cel putin un izomorfism de grupuri.
se numesc izomorfe daca intre ele exista cel putin un izomorfism de grupuri.Daca
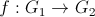 este morfism de grupuri atunci au loc proprietatile:
este morfism de grupuri atunci au loc proprietatile: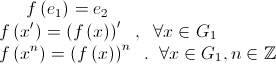
Daca
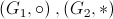 este un izomorfism de grupuri atunci si
este un izomorfism de grupuri atunci si 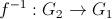 este de asemenea izomorfism de grupuri.
este de asemenea izomorfism de grupuri.Compunerea a doua morfisme de grupuri este morfism de grupuri adica daca
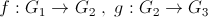 sunt doua morfisme de grupuri atunci si
sunt doua morfisme de grupuri atunci si 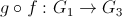 este morfism de grupuri.
este morfism de grupuri.Un morfism
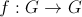 se numeste endomorfism al grupului G.
se numeste endomorfism al grupului G.Un izomorfism
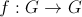 se numeste automorfism al grupului G.
se numeste automorfism al grupului G.Exercitiu:
Pe multimea
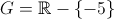 se comsidera legea de compozitie
se comsidera legea de compozitie 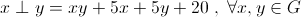 .
.Sa se arate ca functia
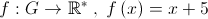 este izomorfism intre grupurile
este izomorfism intre grupurile 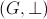 si
si 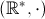 .
.
