Legi de compozitie pe o multime
Definitie:Fie M o multime nevida.
O functie
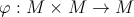 se numeste lege de compozitie (operatie algebrica) pe multimea M.
se numeste lege de compozitie (operatie algebrica) pe multimea M.Elementul
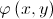 se numeste compusul lui x cu y prin legea de compozitie.
se numeste compusul lui x cu y prin legea de compozitie.Pentru legile de compozitie se folosesc diferite notatii cum ar fi:
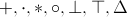 etc.
etc.Exemple:
1)Operatia de adunare a numerelor reale este lege de compozitie pe multimea numerelor reale R.
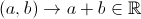
2)Operatia de inmultire a numerelor reale este lege de compozitie pe multimea numerelor reale R.
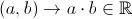
3)Operatia de adunare a matricelor patratice de ordinul doi este lege de compozitie pe multimea
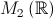 .
.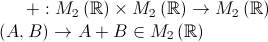
4)Operatia
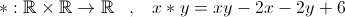 este lege de compozitie pe multimea numerelor reale R.
este lege de compozitie pe multimea numerelor reale R.Proprietati ale legilor de compozitie
AsociativitateaLegea de compozitie * se numeste asociativa pe multimea M daca:
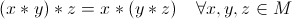
Legea de compozitie * se numeste comutativa pe multimea M daca:
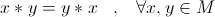
Legea de compozitie * admite element neutru pe multimea M daca exista
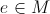 astfel incat:
astfel incat:
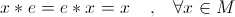
Un element
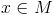 se numeste simetrizabil in raport cu legea de compozitie * daca exista x' in M astfel incat:
se numeste simetrizabil in raport cu legea de compozitie * daca exista x' in M astfel incat:
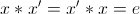
Grupuri
Definitie:Fie G o multime nevida pe care s-a dat o lege de compozitie *.
Spunem ca perechea
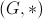 formeaza o structura algebrica de grup daca sunt indeplinite conditiile:
formeaza o structura algebrica de grup daca sunt indeplinite conditiile:G1)Legea * este asociativa;
G2)Legea * are element neutru;
G3)Orice element din G este simetrizabil in raport cu legea *;
Conditiile G1,G2,G3 se numesc axiomele grupului.
In plus daca este indeplinita si axioma G4 se spune ca grupul
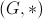 este comutativ sau abelian.
G4)Legea * este comutativa.
este comutativ sau abelian.
G4)Legea * este comutativa.