Titularizare matematica 2010 subiecte rezolvate

Va aflati aici:
Acasa--Profesori--Titularizare matematica 2010--Subiectul 2 ex.3

Vezi enunturile matematica ale subiectelor date la "Concursul national de ocupare a posturilor didactice declarate vacante/rezervate in invatamantul preuniversitar 14 iulie 2010"

Subiectul 2-Exercitiul 3-titularizare matematica 2010
Enunt:

Rezolvare:

a)Calculam derivata functiei f

$f'\left ( x \right )=\left ( ln\left ( 1+x \right )-x+\frac{1}{2}x^2 \right )'=\frac{1}{1+x}-1+x=$
$=\frac{1-1-x+x+x^2}{1+x}=\frac{x^2}{1+x},\forall x\geq 0$

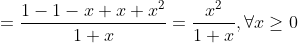
Observam ca $f'\left ( x \right )\geq0,\forall x \geq0$ si $f'\left ( x \right )=0 \Leftrightarrow x=0$ deci functia este strict crescatoare pe $[0,+\infty)$

Tabelul de variatie al functiei este:

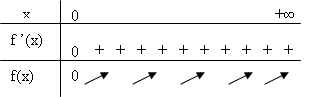
Din tabelul de variatie rezulta ca functia f are un singur punct de extrem local x=0 (punct de minim local).
b)Cautam asimptote orizontale

$\underset{x \to +\infty }{lim}f\left ( x \right )= \underset{x \to +\infty }{lim} \left [ ln \left ( 1+x \right )-x+\frac{1}{2}x^2 \right] =\\= \underset{x \to +\infty }{lim}x\left [ \frac{ln\left ( 1+x \right )}{x} -1+\frac{1}{2}x \right]= \infty\left ( 0-1+\infty \right )=+\infty$

deci graficul functiei nu are asimptota orizontala la plus infinit.
Asimptote oblice

$m=\underset{x \to +\infty }{lim}\frac{f\left ( x \right )}{x}=\underset{x \to +\infty }{lim}\left [ \frac{ln\left ( 1+x \right )}{x} -1+\frac{1}{2}x\right ]=0-1+\infty=+\infty$

deci graficul functiei nu are asimptota oblica.
Deoarece functia data este continua pe intervalul $\left[0,+\infty \right )$ rezulta ca graficul nu are asimptota verticala.
c)Din tabelul de variatie al functiei f facut la punctul a) rezulta ca functia $f\left ( x \right )>0,\forall x>0 \Leftrightarrow$
$\Leftrightarrow ln\left ( 1+x \right )-x+\frac{1}{2}x^2>0,\forall x>0\Leftrightarrow x-\frac{1}{x^2}<ln\left ( 1+x \right ),\forall x>0$
deci prima parte a inegalitatii din enunt este demonstrata.
Pentru a demonstra a doua parte a inegalitatii consideram functia

$g:\left [0,+\infty \right ) \to \mathbb{R},g\left ( x \right )=ln\left ( 1+x \right )-x$

Calculam derivata functiei g:

$g'\left ( x \right )=\frac{1}{1+x}-1=\frac{1-1-x}{1+x}=\frac{-x}{1+x}\leq 0,\forall x\geq 0$

Observam ca $g'\left ( x \right )\leq 0,\forall x \geq 0$ si $g'\left ( x \right )= 0\Leftrightarrow x = 0$
deci functia g este strict descrescatoare pe domeniul de definitie

$\Rightarrow g\left ( x \right )<g\left ( 0 \right )=0,\forall x>0 \Rightarrow ln \left ( 1+x \right )-x<0,\forall x>0$ $\Rightarrow ln\left ( 1+x \right )<x,\forall x>0$

deci si a doua parte a inegalitatii din enunt este demonstrata.

d)In inegalitatea de la punctul c) dam lui x valorile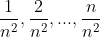 $\frac{1}{n^2},\frac{2}{n^2},...,\frac{n}{n^2}$
si adunam inegalitatile obtinute:

$\frac{1}{n^2}-\frac{1}{2}\left ( \frac{1}{n^2} \right )^2<ln\left ( 1+\frac{1}{n^2} \right )<\frac{1}{n^2}\\ \frac{2}{n^2}-\frac{1}{2}\left ( \frac{2}{n^2} \right )^2<ln\left ( 1+\frac{2}{n^2} \right )<\frac{2}{n^2}\\ ..........................................................\\ \frac{n}{n^2}-\frac{1}{2}\left ( \frac{n}{n^2} \right )^2<ln\left ( 1+\frac{n}{n^2} \right )<\frac{n}{n^2}\\$

$\frac{1+2+...+n}{n^2}-\frac{1}{2}\cdot \frac{1^2+2^2+...+n^2}{n^4}<\\<ln\left ( 1+\frac{1}{n^2} \right )\cdot \left ( 1+\frac{2}{n^2} \right )\cdot ...\cdot \left ( 1+\frac{n}{n^2} \right ) <\frac{1+2+...+n}{n^2}$

ceea ce este echivelant cu

$\underset{tinde \; la \; \frac{1}{2}}{\underbrace{\frac{n+1}{2n}-\frac{1}{2}\cdot \frac{\left ( n+1 \right )\left ( 2n+1 \right )}{6n^3}}}{ } < ln\left ( 1+\frac{1}{n^2} \right )\cdot \left ( 1+\frac{2}{n^2} \right )\cdot...\cdot\left ( 1+\frac{n}{n^2} \right )<\\ <\underset{tinde \; la \; \frac{1}{2}}{\underbrace{\frac{n+1}{2n}}}$
si folosind criteriul clestelui rezulta ca limita ceruta in exercitiu este egala cu $\frac{1}{2}$

Vezi baremul de corectare si notare pentru examenul de titularizare la matematica din 14 iulie 2010. Vezi baremul de corectare si notare pentru examenul de titularizare la matematica din 14 iulie 2010.

Vezi celelalte comentarii (0)

Propune un material nou in format pdf sau doc pe site

Adauga un comentariu
Nume:
Comentariu:
Verificare antispam:

Titularizare matematica 2010

Subiectul 2-Exercitiul 3-titularizare matematica 2010 Enunt: Rezolvare:

Subiectul 2-Exercitiul 3-titularizare matematica 2010
Enunt:

Rezolvare: