Titularizare matematica 2010

Va aflati aici:
Acasa--Profesori--Titularizare matematica 2010--Subiectul 1 ex.1
Vezi enunturile matematica ale subiectelor date la "Concursul national de ocupare a posturilor didactice declarate vacante/rezervate in invatamantul preuniversitar 14 iulie 2010"

Subiectul 1-Exercitiul 1-titularizare matematica 2010
Enunt:

Rezolvare:

a)Fie A={1,4,6}

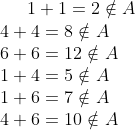
rezulta ca multimea A are proprietatea (p).
Fie B={1,3,6}
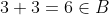deci multimea B nu are proprietatea (p).
b)Exemplul 1
Fie multimea C={1,3,5,...,2009} care are 1005 elemente si care este inclusa in multimea data in enunt.
Suma oricaror doua elemente din C,nu neaparat distincte,este numar par deci nu apartine multimii C.
In concluzie,multimea C are proprietatea (p).
Exemplul 2
Fie multimea D={1006,1007,...,2010} care are 1005 elemente si este inclusa in multimea data in enunt.
Pentru oricare doua elemente x,y din D nu neaparat distincte,avem .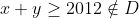
In concluzie multimea D nu are proprietatea (p).
c)Fie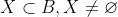 o multime care nu are proprietatea (p).
Rezulta ca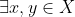 nu neaparat distincte,astfel incat .
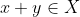Din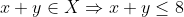
Din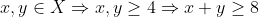
Din cele doua relatii de mai sus obtinem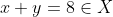 si cum x,y sunt din multimea 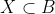rezulta ca x=4 si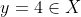
Concluzie {4,8}.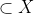
Asadar avem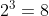 multimi nevide care nu au proprietatea (p).
Multimea B={4,5,6,7,8} are in total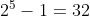 submultimi nevide si cum am stabilit mai sus ca 8 submultimi nu au proprietatea (p) rezulta ca restul de 31-8=23 submultimi nevide au proprietatea (p).
d)Fie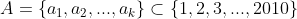 o multime care are proprietatea (p).Putem presupune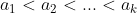
Notam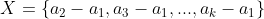
Cum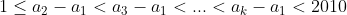 rezulta
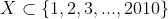si X are k-1 elemente.
Sa observam ca multimile A si X sunt disjuncte.
Intr-adevar sa presupunem prin reducere la absurd ca multimile A si X ar avea un element comun.
Rezulta ca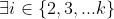 si 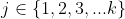astfel incat
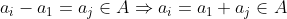ceea ce este o contradictie deoarece multimea A are proprietatea (p).
Deci .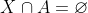
Multimea A are k elemente.
Multimea X are k-1 elemente.
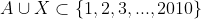deci .
Folosim egalitatea si obtinem

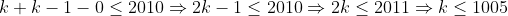
c.c.t.d.
Vezi baremul de corectare si notare pentru examenul de titularizare la matematica din 14 iulie 2010.