Va aflati aici:
Acasa--Profesori--Titularizare matematica 2010--Subiectul 1 ex.2
Vezi enunturile matematica ale subiectelor date la "Concursul national de ocupare a posturilor didactice declarate vacante/rezervate in invatamantul preuniversitar 14 iulie 2010"
Subiectul 1-Exercitiul 2-titularizare matematica 2010
a)=\frac{AB\cdot dist(C,AB)}{2}=\frac{AC\cdot dist(B,AC)}{2})
}{dist(C,AB)}\leq 1 \Rightarrow dist(B,AC)\leq dist(C,AB))
b)Cum punctele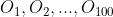 sunt oricare trei necoliniare rezulta ca oricare trei din acestea formeaza un triunghi.
sunt oricare trei necoliniare rezulta ca oricare trei din acestea formeaza un triunghi.
Numarul triunghiurilor care au varfurile in multimea M este egal cu numarul tripletelor (neordonate) de puncte din M.
In concluzie numarul triunghiurilor este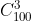
c)Fie d dreapta care intersecteaza cercurile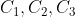 conform ipotezei.
conform ipotezei.
Alegem un reper cartezian in care axa Ox este dreapta d.
In acest reper avem,O_2(x_2,y_2),O_3(x_3,y_3).)
Cum distantele de la punctele la axa Ox sunt cel mult 1 rezulta ca
la axa Ox sunt cel mult 1 rezulta ca 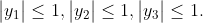
Fara a restrange generalitatea putem presupune ca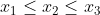 .
.
=\frac{1}{2}\cdot \left | \Delta \right |)
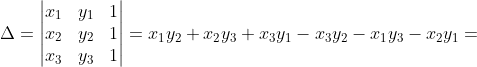
+y_2\left ( x_1-x_3 \right )+y_3\left ( x_2-x_1 \right ) )
Obtinem:
+y_2\left ( x_1-x_3 \right )+y_3\left ( x_2-x_1 \right )\end{vmatrix} \leq )
+ \begin{vmatrix} y_2 \end{vmatrix}\left ( x_3-x_1 \right )+ \begin{vmatrix} y_3 \end{vmatrix}\left ( x_2-x_1 \right ) \leq)
\leq)
^2+\left ( y_3-y_1 \right )^2}=2O_1O_3)
Retinem ca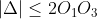
=\frac{O_1O_3 \cdot \cdot h_{O_2} }{2}=\frac{1}{2} \cdot \left | \Delta \right | \leq \frac{1}{2} \cdot2O_1O_3=O_1O_3)
Rezulta:
 ceea ce trebuia demonstrat.
ceea ce trebuia demonstrat.
d)Alegem cea mai mare distanta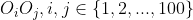
Fie aceasta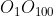 .
.
Daca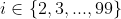 atunci triunghiul
atunci triunghiul 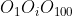 are o inaltime cel mult 2 (conform pct.b)).
are o inaltime cel mult 2 (conform pct.b)).
In triunghiul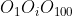 avem
avem 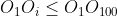 si
si 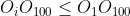 deci conform punctului a) cea mai mica inaltime a triunghiului
deci conform punctului a) cea mai mica inaltime a triunghiului 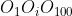 este inaltimea dusa din
este inaltimea dusa din  .
.
Demonstram ca inaltimea dusa din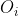 in
in 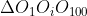 este mai mica sau egala cu 2.
este mai mica sau egala cu 2.
Intr-adevar daca presupunem,prin reducere la absurd,ca inaltimea din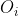 este mai mare ca 2 , atunci toate inaltimile triunghiului vor fi mai mari strict decat 2 , contradictie cu punctul b).
este mai mare ca 2 , atunci toate inaltimile triunghiului vor fi mai mari strict decat 2 , contradictie cu punctul b).
Mai departe deducem ca dreapta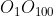 intersecteaza cercul
intersecteaza cercul 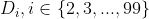 .
.
Cum dreapta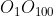 intersecteaza si cercurile
intersecteaza si cercurile 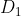 si
si 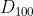 rezulta ca dreapta
rezulta ca dreapta 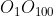 intersecteaza toate cercurile
intersecteaza toate cercurile 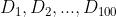 ceea ce trebuia demonstrat.
ceea ce trebuia demonstrat.
Vezi baremul de corectare si notare pentru examenul de titularizare la matematica din 14 iulie 2010.
Acasa--Profesori--Titularizare matematica 2010--Subiectul 1 ex.2
Vezi enunturile matematica ale subiectelor date la "Concursul national de ocupare a posturilor didactice declarate vacante/rezervate in invatamantul preuniversitar 14 iulie 2010"
Subiectul 1-Exercitiul 2-titularizare matematica 2010
Enunt: Rezolvare:
Rezolvare:
a)b)Cum punctele
Numarul triunghiurilor care au varfurile in multimea M este egal cu numarul tripletelor (neordonate) de puncte din M.
In concluzie numarul triunghiurilor este
c)Fie d dreapta care intersecteaza cercurile
Alegem un reper cartezian in care axa Ox este dreapta d.
In acest reper avem
Cum distantele de la punctele
Fara a restrange generalitatea putem presupune ca
Obtinem:
Retinem ca
Rezulta:
d)Alegem cea mai mare distanta
Fie aceasta
Daca
In triunghiul
Demonstram ca inaltimea dusa din
Intr-adevar daca presupunem,prin reducere la absurd,ca inaltimea din
Mai departe deducem ca dreapta
Cum dreapta
Vezi baremul de corectare si notare pentru examenul de titularizare la matematica din 14 iulie 2010.
